The BayesicFitting package offers a general way to fit models to data in a Bayesian way. It consists of 3 families of classes: the Model classes, the Fitter classes and the NestedSampling classes.
This is not the place to explain either the mathematics behind Bayesian modelling of data or the algorithms used. For the mathematics look at the books of Sivia, Bishop, von der Linden and Jaynes and for some fitter algorithms Press.
The Model classes define the model functions which are to be fitted. A model class has methods to return its function value and partial derivates given one input value and a set of parameters. It is also the place where the parameters and standard deviations are stored once they are fitted. Limits on the allowed parameter range belong to the model domain too. Just like fixed parameters.
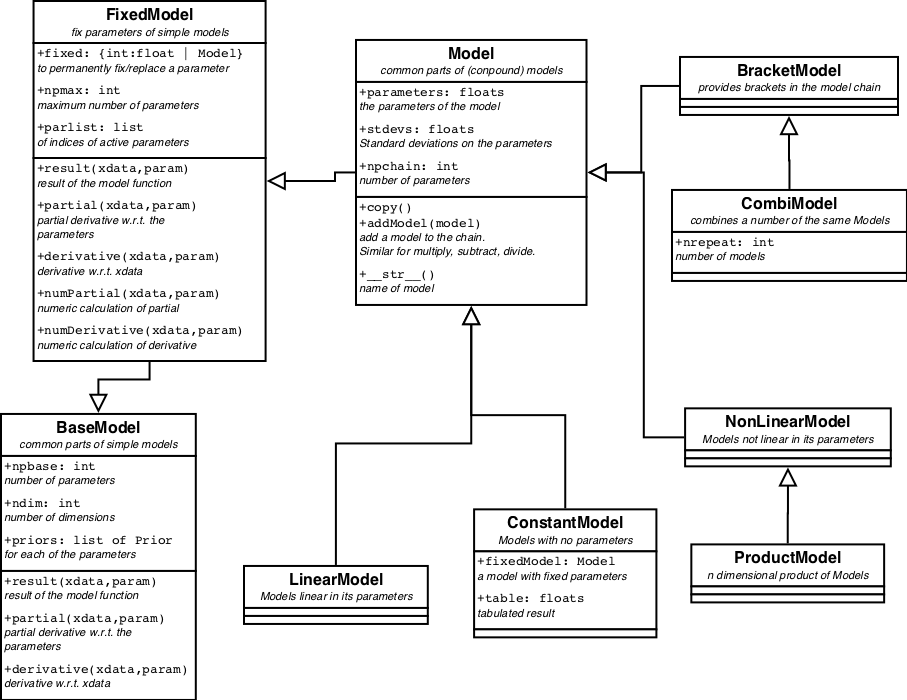
A partial and schematic view on the model classes and their relationships can be found in figure 1.
For all images it holds that the boxes are classes. In the upper panel the name, in the mid panel some of the attributes of the class and in the lower panel some methods. Not all attributes and methods are displayed. An open arrow indicates inheritance: Model inherits from FixedModel which inherits from BaseModel. A black arrow indicates a relationship between the classes, which is written next to it.

BaseModel defines a simple or basic model and all its methods.
A basic model has methods to return the functional result,
y = f( x:p ), where p represents the parameters; it is an array (or
list) of K floats. x is the independent variable. It can have any length,
even being a single number. If the model is more-dimensional, x needs to
have 2 dimensions, an array of points in a more-dimensional space. The
shape of x is N or (N,D), where N is the number of points and D (>=2) is
the dimensionality. y is the result of the function. It has a length of
N, irrespective of the dimensionality of the model.
If the BaseModel can handle it, the x variable can even be a list of
different types. No pre-defined model in this package is like that, but
a user might see some usage for it.
BaseModel also defines the partial derivatives of f to p, ∂f(x:p) / ∂p and derivatives of f to x. The shapes are resp. (N,K) and N or (N,D). When no (partial) derivatives can be calculated, this class automatically provides numerical (partial) derivatives. The derivative, ∂f / ∂x, is only used when models are connected via a pipe operation. See Model. However, the partials, ∂f / ∂p, are intensively used by the fitters to feel its ways towards the minimum.
Each BaseModel provides its own name and names for its parameters.
BaseModels reach out to concrete implementations of simple models,
see Figures 2 and 3, via methods called baseResult, basePartial,
baseDerivative and baseName, to get the there implemented result,
partial etc.
In each BaseModel one or more parameters can be replaced either by a constant or by another Model. This is handled in FixedModel. For each fixed parameter, the model loses one item in the parameter list. When the parameter is replaced by a Model, the parameters of the Model are appended to the BaseModels parameter list; in the same order as they are provided.
FixedModels stay fixed for as long as the object exists. Consequently they can only be constructed when the BaseModel itself is constructed. Models can only be fixed up on construction.
Results and partial derivatives for FixedModels are calculated from the constituent Models. The derivative to the independent variable cannot be calculated in general. They are replaced by numeric derivatives.
A FixedModel is still a simple model, even though quite elaborate functionality can be constructed this way.
In the center of the tree sits Model, the last common anchestor
of the model classes. It is the class that fitters and nested sampling
work up on. A Model needs to define all methods that the fitters
might need, in particular the methods result( xdata, parameters ) and
partial( xdata, parameters ), where xdata and parameters are the x
and p in f( x:p ) as defined above.
It also contains methods for keeping some of the parameters fixed, temporarily during the fitting, for checking for positivity of some parameters and/or non-zeroness and for applying limits on the parameters.
Two or more models can be concatinated to form a new compound model with
model1 + model2. The result equals the sum
of the individual results. The parameters are listed with the ones from
model1 first, followed by those of model2, etc. Other arithmetic
operators (-*/|) can be used too, with obvious results.
The methods of a compound model are called recursively over the chain.
For every (simple) model in a chain. relevant information is kept within the Model itself: lists of parameters, standard deviations (when available) and Priors. The latter one is only seriously used when the Model is used in NestedSampler.
After the Model things starts to diversify into different directions, LinearModel and NonLinearModel, the BracketModel and the ConstantModel.
BracketModel provides brackets () in the model chain. It enables to distinguish between m1 * m2 + m3 and m1 * (m2 + m3). In the model chain the models are handled strictly left to right, so m1 + m2 * m3 is implemented as (m1 + m2 ) * m3. The BracketModel can change the order of calculation where that is needed.
A CombiModel combines a fixed number of Models into one, while maintaining certain relations between similar parameters. E.g. to fit a triplet of lines in a spectrum, combine 3 line models (GaussModel) into a CombiModel with all the same linewidths and the known distances of the lines in the triplet. This way there are only 5 parameters (3 amplitudes, 1 position and 1 width) to be fitted. See Example (TBD)
ConstantModel is the first concrete child of Model. It returns a constant form, no matter what the input. The constant form could be 0 everywhere, but also another Model with known parameters, or even a table.
LinearModels are linear in its parameters, meaning that the result
of a concrete linear model is the inner product of the partial
derivatives with the parameters. This operation is defined in this
class. Consequently concrete linear models only need to define the
partials as basePartial.
All pre-defined linear models are displayed in figure 2
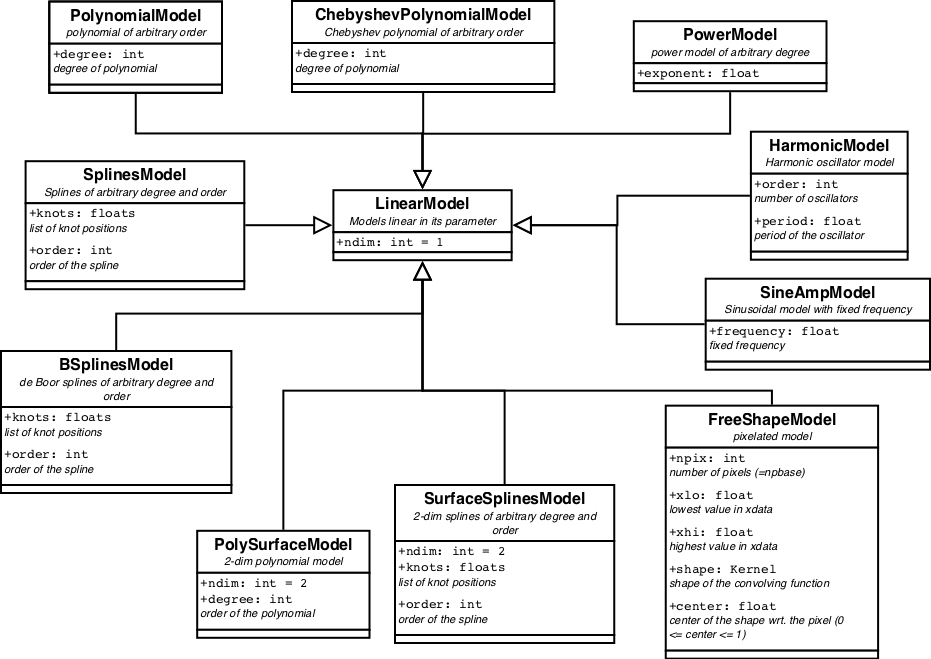
LinearModels have quite some benefits. Using a Gaussian error distribution (aka least squares) the optimal parameters can be found directly by inverting the Hessian matrix. Computationally there are several methods to achieve it, which are all relatively simple. They are implemented in the linear fitter classes. Another benefit is that the posterior for the parameters is also a multidimensional Gaussian, which is completely characterized by its covariance matrix and can be easily integrated to obtain the evidence.
It is not wrong to use a non-linear fitter on a linear model. Sometimes it can even be necessary e.g. when the number of parameters gets large.
All Models that are not linear are NonLinearModels. They at
least need to define the result as baseResult. When basePartial or
baseDerivative is not implemented, numeric approximations are used.
All pre-defined non-linear models are displayed in figure 3
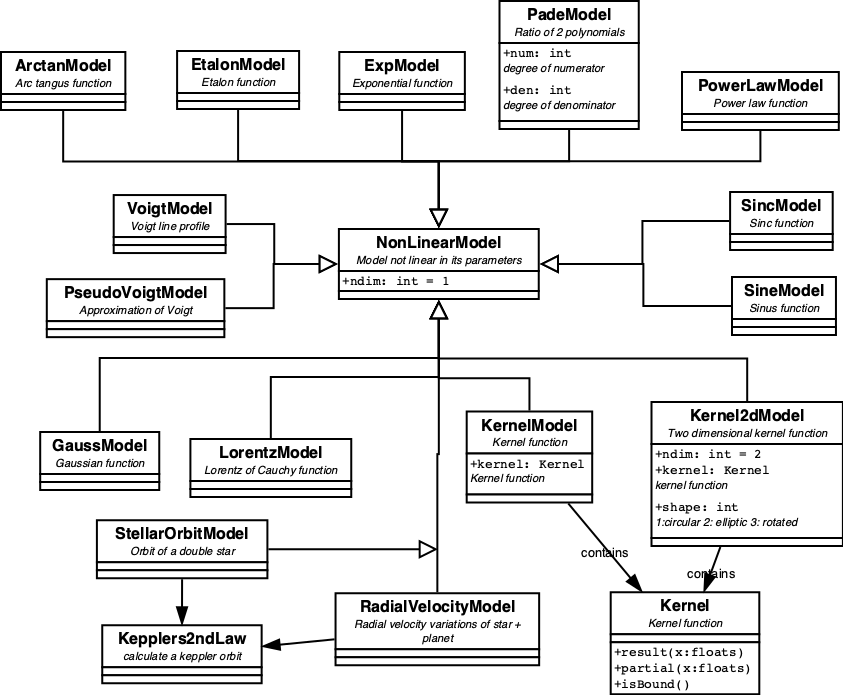
NonLinearModels need non-linear (NL) fitters to optimize their parameters. As NL fitters are iterative, more complicated, slower and not guaranteed to find the best solution, NonLinearModels are harder to handle.
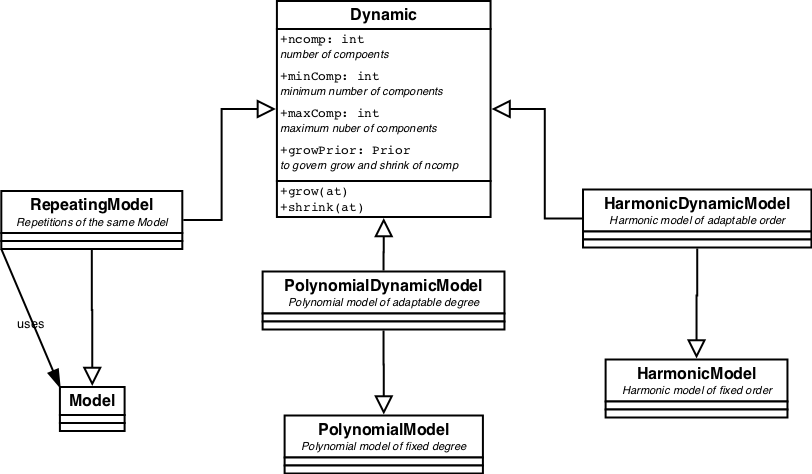
Dynamic models are specialisations of Models that have a fixed attribute. E.g PolynomialModel with fixed degree or HarmonicModel with fixed order. Dynamic implements methods to let the model grow or shrink. These models can not be used with ordinary Fitters. Using NestedSampler they automatically converge on the model with the optimal number of components.
All pre-defined Dynamic models are displayed in figure 4.
A special case of NonLinearModels are the KernelModels and their more-dimensional variants, Kernel2dModel. A KernelModel encapsulates a Kernel function, which is defined as an even function with a definite integral over (-inf,+inf).
All pre-defined kernels are displayed in figure 5.
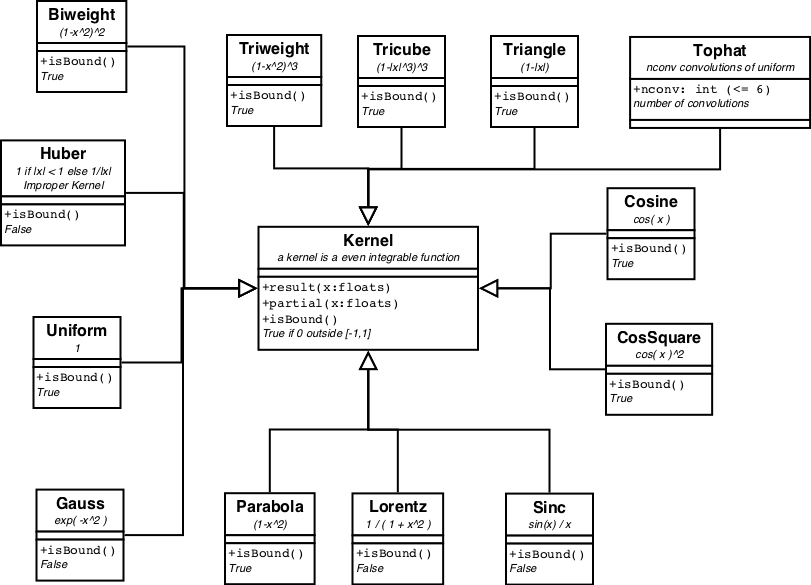
Of the more-dimensional variants, only the 2-dim is defined, where the 2d kernel is either round or elliptic along the axes, or rotated elliptic. For more-dimensional kernels some kind of rotational matrix needs to be defined. It more or less waits for a real case where it is needed.
Note that GaussModel and LorentzModel could both be implemented as a KernelModel, while SincModel actually is a wrapper around a KernelModel.
If the needed model can not be constructed via the fixing of
parameters or by concatenating models, it is
advised to take a similar (linear or non-linear) model as an example and
change the revelant methods. As a bare minimum the method baseResult
need to be filled. The method basePartial either needs to be filled or
the method should be removed. In the latter case numeric derivatives are
used.
The method testPartial in Model can be used to check the
consistency between the methods baseResult and basePartial.
When a new model is constructed either from existing ones or new, it is the users responsibility to make sure the the parameters are not degenerate, i.e. measuring essentially the same thing.
The root of the fitter classes is BaseFitter, a large class containing the common methods for parameter fitting. Mostly these are methods using the covariance matrix, like calculating the standard deviations or the confidence regions of the fit. And most importantly the calculation of the evidence. This is done by a Gaussian approximation of the posterior, also known as Laplace's method. For the prior a UniformPrior is asumed, for which limits are necessary to make it a proper probability. The limits need to be provided by the user.
In case of parameter estimation of a LinearModel Laplace's method is exact, provided that the limits on the parameters are wide enough. In all other cases it is an approximation, better or worse depending on the problem at hand. Nontheless it can be used succesfully in model comparison when some reasonable provisions are taken into account, like comparing not too different models, feeding the same data (and weights) to all models etc.
The Fitter inheritance tree is displayed in figure 6.
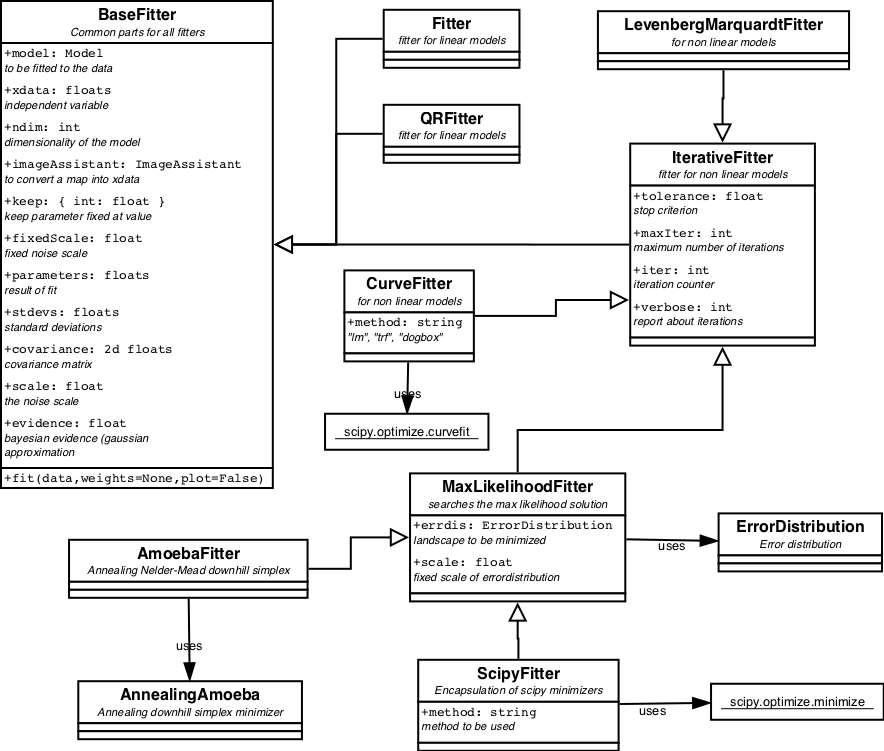
The package contains 2 linear fitter classes: Fitter and QRFitter. The former applies LU-decomposition of the Hessian matrix and is best for solving single problems. The latter applies a QR-decomposition of the Hessian. When the same problem needs to be solved for several different datasets QR-decomposition is more efficient.
A third method, Singular Value Decomposition (SVD), is somewhat more robust when the Hessian is nearly singular. SVD decomposes the design matrix into a singular value decomposition. Those singular values which do not exceed a threshold are set to zero. As a consequence the degenerate parameters get values which are minimalised in a absolute sense.
The SVD-Fitter is TBW.
The other descendants of the BaseFitter are all iterative fitters to be used with non-linear models. IterativeFitter implements a number of methods common to all non-linear fitters.
Non-linear fitters are iterative, take more time and have no guarantee that it will find the global optimal. Most NL fitters fall in the first local minimum and can not escape from there. These fitters can only be used effectively on problems where the global minimum is close by; either because the problem has only one minimum (it is monomodal), or the initial parameters are close to the final global minimum. When uncertain about it, one could start the fitter at widely different initial positions and see whether it ends up at the same location.
The LevenbergMarquardtFitter is an implementation of Levenberg-Marquardt algorithm from Numerical Recipes par. 15.5. It actively uses the partial derivatives. The LevenbergMarquardtFitter will go downhill from its starting point, ending wherever it will find a minimum. Whether the minumum is local or global is unclear.
CurveFitter ecapsulates the method scipy.optimize.curvefit. See
curvefit
for details.
Up to now all fitters try to find the minimum in the χ2-landscape. They are strictly "least squares". MaxLikelihoodFitters can also maximize the log likelihood of a selected ErrorDistribution.
The AmoebaFitter performs the simplex method described in AnnealingAmoeba to find the minimum in χ2 or the maximum in the likelihood.
AnnealingAmoeba implements the simplex method designed by Nelder and Mead to find the minimum value in a functional landscape. In its simple invocation with temperature = 0, it proceeds downhill only in the functional landscape. Steps where the value increases are refused so it falls and stays in the first minimum it encounters. In that respect it has the same limitations as the LevenbergMarquardtFitter.
The implementation here adds Metropolis annealing to it: Depending on the temperature it sometimes takes steps in the uphill direction, while downhill steps are always taken. Gradually the temperature diminishes. This way it might escape from local minima and find the global minimum. No guarantee however. In doubt start it at different initial values etc.
AnnealingAmoeba evolved from earlier implementations of the Nelder-Mead algorithm in [Press][5] par 10.4 and 10.9.
The method scipy.optimize.minimize implements about 10 minimization
algorithms. ScipyFitter encapsulates the minimize method and call
the algorithms by their name. However there are also 10 named fitters
all residing within ScipyFitter.
They are presented here as is. We dont have much experience with most of them, except with the ConjugateGradientFitter.
The ConjugateGradientFitter is especially usefull when there are many
(>20) parameters to be fitted, as it does not require matrix
manipulations. For models with very many parameters (>10000) where
construction of the Hessian matrix starts to run out of memory, it is
possible to implement the gradient method directly in the model.
The others are NelderMeadFitter, PowellFitter, BfgsFitter, NewtonCGFitter, LbfgsFitter, TncFitter, CobylaFitter, SlsqpFitter, DoglegFitter and TrustNcgFitter.
For details on the individual ScipyFitters see minimize
In real life data often outliers are present, little understood large excursions from the general trend. It also can occur that some parts of the data need to be excluded from the fit, e.g. because at those places there is flux and the fit should be only to the background. In those cases RobustShell is usefull. RobustShell is a shell around a Fitter. In an iterative way it de-weights the outliers. Kernel functions can be used as de-weighting schemes.
Robust fitting is even more error prone than normal fitting. Always carefully check the results.
Nested Sampling is an algorithm invented by David MacKay and John Skilling, to integrate the posterior to obtain the evidence. At the same time samples from the posterior are collected into a SampleList. NestedSampler follows the core algorithm as presented in [Sivia][1] closely, but is expanded with pluggable Problems, Models, Priors, ErrorDistributions and Engines. It offers solutions to a wide variety of inverse problems.
Initially an ensemble of trial points, a WalkerList, in the space spanned by the (hyper)parameters is randomly distributed over the Priors of the parameters. These points are Walkers and typically there are 100 of them. In an iterative loop, the walker with the lowest likelihood is removed from the ensemble of walkers. It is weighted and stored as a Sample in a SamleList. One of the remaining walkers is copied and randomly moved around by Engines, provided that its likelihood stays higher than that of the stored Sample. This way the walkers slowly climb to the maximum value of the likelihood. The stored Samples provide enough pointers into the Likelihood function to make a good estimate of the integral (evidence).
The classes associated with NestedSampler are displayed in figure 7.
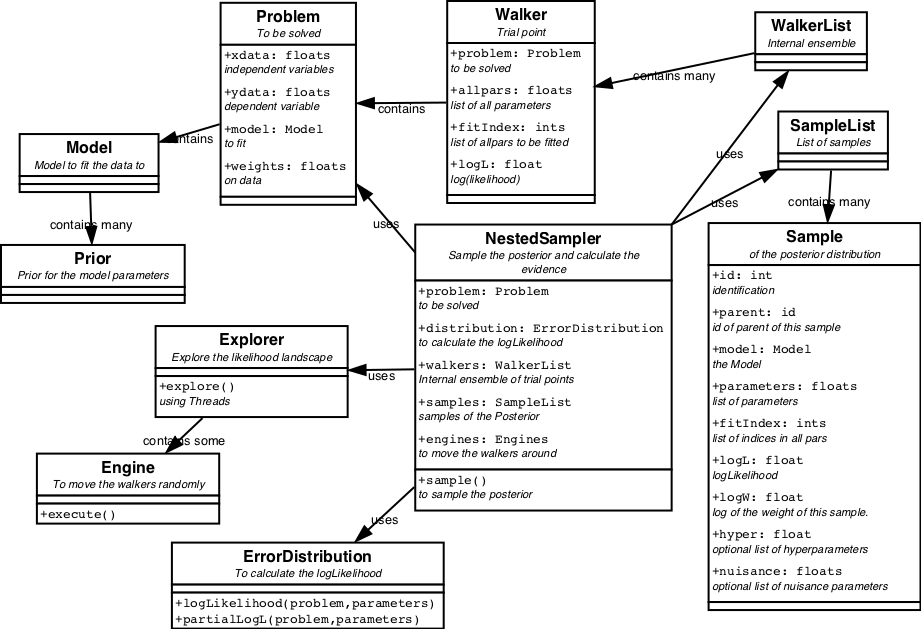
NestedSampler acts upon a Problem. A Problem is a object that encodes a solvable problem. This is meant in a very broad sense. The solution of the problem is contained in the parameters. Together with (special) ErrorDistribution, Engines and Priors, NestedSampler can optimize the parameters. What the Problem, parameters, etc. exactly are, is completely dependent on the problem to be solved.
In versions 1.0 of this package and below, only problems with parameterized models, one or more dimensional input and one-dimensional outputs were handled. For these kind of problems ClassicProblem is introduced. Mostly it stays behind the scenes and is invisible for the users.
More Problems can be found in figure 8.
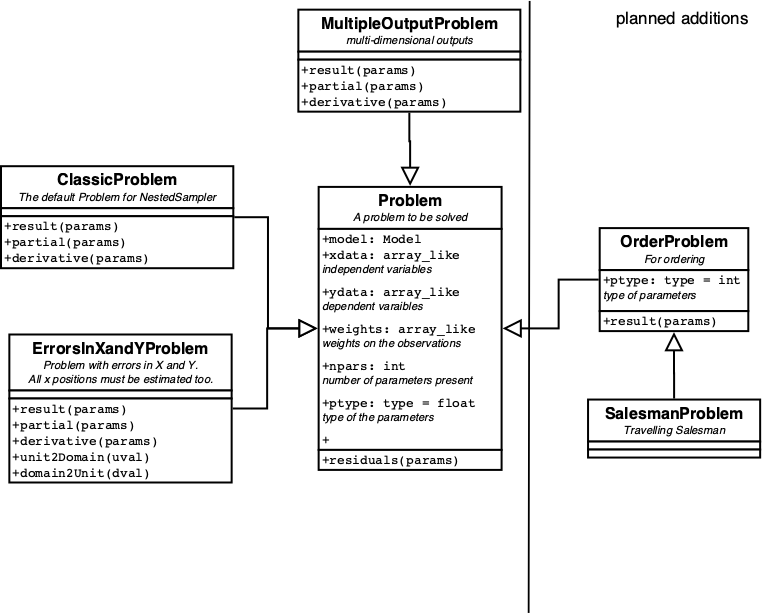
A Problem knows how to calculate its result, partial and derivative given the parameters. It also knows which Engines and which ErrorDistribution is the best choice.
The ClassicProblem has a Model, containing a list of parameters, each
of which has a Prior. Together with the xdata, the ydata and the
optional weights, the likelihood can be calculated by the
ErrorDistribution. The ErrorDistribution itself might have
HyperParameters, that have to be estimated too. Finally there is the
Explorer which explores the likelihood via various Engines.
The Priors contain information about the parameters which is known before the data is taken into account. It is the range that the parameters can move, without being frowned up on.
The predefined Priors are displayed in figure 9.
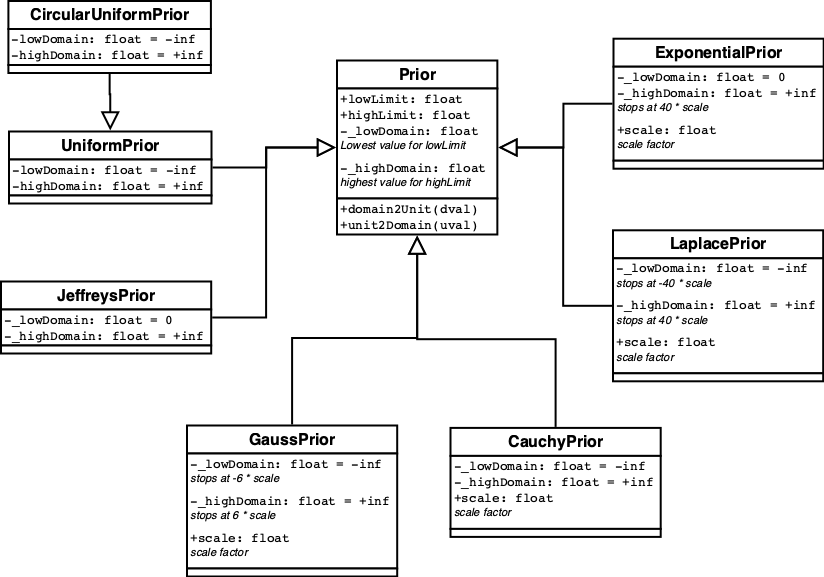
All Priors define two methods unit2domain which transforms
(random) value in [0,1] into a (random) value from the prior
distribution, and its inverse domain2unit.
The main task of the ErrorDistribution is to calculate the likelihood, or better the log thereof. The partial derivative of the logLikelihood wrt the parameters is also defined. It is used in the Engine of choice for parameter with continuous values: GalileanEngine.
The predefined ErrorDistributions are displayed in figure 10.
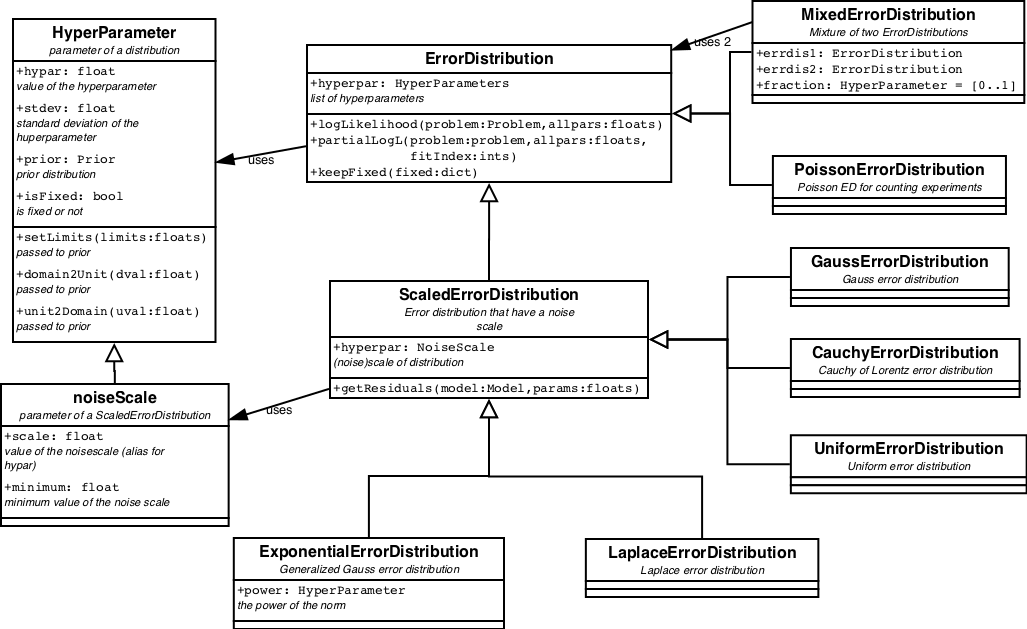
Some ErrorDistributions have parameters of themselves, so called HyperParameters. One special case is the NoiseScale.
The NoiseScale contains information about the amount of noise in the data. This can be in the form of a fixed number, claimimg that the amount of noise is known beforehand. Or it can be in the form of a prior. As the amount of noise is a positive definite number, the non-informative prior for it is the JeffreysPrior. The JeffreysPrior is, like the UniformPrior, an improper prior, which means that its integral is unbound. Low and high limits (both > 0) need to be provided when calculating the evidence.
The way the walkers are moved around in the available parameter space is determined by the Engines. Several Engines are availble: ""ChordEngine, **GalileanEngine, GibbsEngine, CrossEngine and StepEngine. For DynamicModels BirthEngine and DeathEngine are needed too.
The available Engines are displayed in figure 11.
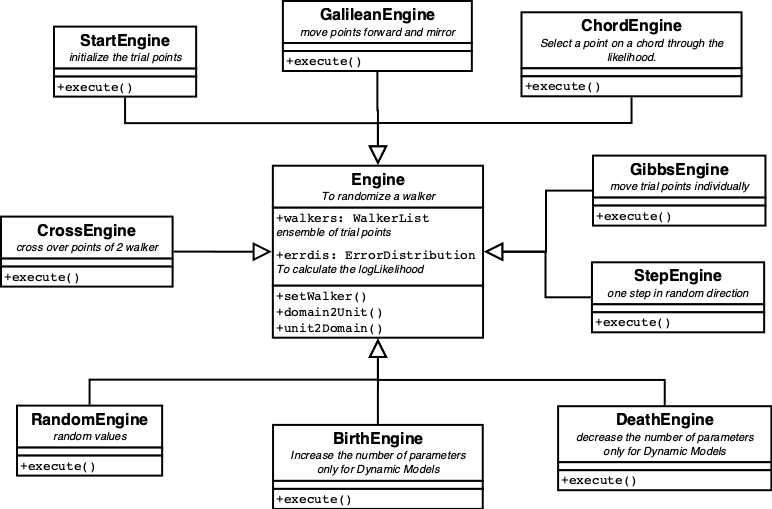
Two need special mentioning. The StartEngine generates the initial random ensemble. The GalileanEngine moves the point in a random direction for several steps. When the walker is moving outside the area defined by the lowest likelihood, the direction is mirrored on the likelihood boundary. The GalileanEngine is the most efficient engine.