83 Aquarii
83 Aqr is a visible double star with a period of about 20 years and aseparation of 0.2 arcsec.
We have data from SIDONIE (https://sidonie.oca.eu) and WDS
(https://www.usno.navy.mil/USNO/astrometry/optical-IR-prod/wds/int4)
Author: Do Kester
We need to import some classes
In[1]:
import numpy as numpy import math from astropy.io import ascii from BayesicFitting import StellarOrbitModel from BayesicFitting import MultipleOutputProblem from BayesicFitting import PolynomialModel from BayesicFitting import CircularUniformPrior from BayesicFitting import NestedSampler from BayesicFitting import formatter as fmt from BayesicFitting import plotFit from BayesicFitting import Tools import matplotlib.pyplot as plt
In[2]:
#%matplotlib osx
Read the data
In[3]:
tbl = ascii.read( "/Users/do/Projects/DoubleStars/83Aqr/83Aqr.dat", include_names=['Date', 'Angle',
'Separ', 'err-a', 'err-s', 'nts', 'pr'] )
# print( tbl )
# The table lists:
# fractional years
# angle in degree
# separation in arcsec
# number of nights the star is observed
# precision in number of decimals in the separation (2 or 3)
yr0 = tbl['Date'].data
phi = tbl['Angle'].data
dis = tbl['Separ'].data
erp = tbl['err-a']
erd = tbl['err-s']
nts = tbl['nts'].data
prc = tbl['pr'].data
#phi = numpy.where( phi > 300, phi - 360, phi )
In[4]:
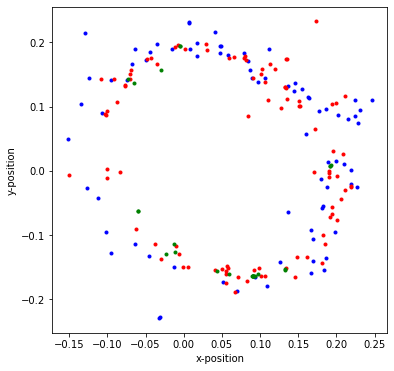
th = phi * math.pi / 180 ## Do we need a correction for leap years. They are 0.3% longer yr1 = yr0 - 1900 #xpos = dis * numpy.cos( th ) #ypos = dis * numpy.sin( th ) xpos = dis * numpy.sin( th ) ypos =-dis * numpy.cos( th ) plt.figure( "data", figsize=(6,6) ) q = numpy.where( yr0 <= 1900 ) plt.plot( xpos[q], ypos[q], 'k.' ) q = numpy.where( numpy.logical_and( 1900 <= yr0, yr0 < 1950 ) ) plt.plot( xpos[q], ypos[q], 'b.' ) q = numpy.where( numpy.logical_and( 1950 <= yr0, yr0 < 2000 ) ) plt.plot( xpos[q], ypos[q], 'r.' ) q = numpy.where( yr0 >= 2000 ) plt.plot( xpos[q], ypos[q], 'g.' ) plt.xlabel( 'x-position' ) plt.ylabel( 'y-position' ) plt.show()
Out[4]:
A bit of data massaging.
In[5]:
## Do we need a correction for leap years. They are 0.3% longer yr = yr0 - 1900 # Make weights proportional to the number of nights observed and # divide by 4 if the precision is given in 2 decimals in stead of 3 #wgt = numpy.where( prc == 3, nts, nts / 4 ) #wgt = numpy.sqrt( nts ) * numpy.power( 10.0, prc - 3 ) erd = numpy.where( erd == 0, 100, erd ) #wgt = nts / ( numpy.square( 100 * erd )) rwgt = nts / ( 100 * erd ) rwgt = numpy.where( rwgt > 30, 30.0, rwgt ) rwgt = numpy.where( prc == 0, 0.0, rwgt ) erc = numpy.array( [100, 10, 5, 2, 1], dtype=float ) erp = numpy.where( erp == 0, erc[prc], erp ) pwgt = nts / erp pwgt = numpy.where( prc == 0, 0.0, pwgt ) pwgt *= 0.1 ## to balance with rwgt d2r = math.pi / 180 pwgt *= d2r # Combine xpos and ypos into a 2-d array: pos pos = numpy.append( dis, th ).reshape( 2, -1 ).transpose() wgt = numpy.append( rwgt, pwgt ).reshape( 2, -1 ).transpose()
We define a stellar orbit model. It has 7 parameters: eccentricity,
semimajor axis, period, periastron phase, inclination of the orbit,
longitude of ascending node and phase of the ascending node.
All 4 phase parameters get a CircularUniformPrior 0 to 2 pi.
In[6]:
twopi = 2 * math.pi mdl = StellarOrbitModel( spherical=True ) ## eccen, semimaj, period, phase, inclin, node phase, node pos lolim = [0.0, 0.0, 20.0] hilim = [0.9, 1.0, 30.0] mdl.setLimits( lowLimits=lolim, highLimits=hilim ) #Tools.printclass( mdl ) mdl.setPrior( 3, prior=CircularUniformPrior(), limits=[0,twopi] ) ## phase of periastron mdl.setPrior( 4, prior=CircularUniformPrior(), limits=[0,math.pi] ) ## inclination mdl.setPrior( 5, prior=CircularUniformPrior(), limits=[0,math.pi] ) ## from North to line of nodes mdl.setPrior( 6, prior=CircularUniformPrior(), limits=[0,twopi] ) ## fron line of nodes to periastron #Tools.printclass( mdl )
Define a MultipleOutputProblem which reorganises the multiple outputs:
(x,y) into a 1-d array that can be handled by the NestedSampler.
Define NestedSampler with extended ensemble for better precision.
In[7]:
problem = MultipleOutputProblem( model=mdl, xdata=yr, ydata=pos,
weights=wgt )
# define NestedSampler
ns = NestedSampler( problem=problem, seed=80409 )
ns.ensemble = 500
#ns.engines[0].verbose = 5
# set limits on the noise scale of the distribution
ns.distribution.setLimits( [0.01,100] )
# ns.verbose = 2
# run NestedSampler
evi = ns.sample( )
Out[7]:
Fit all parameters of StellarOrbit Using a Gauss error distribution with with unknown scale Moving the walkers with GalileanEngine ChordEngine >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> Iteration logZ H LowL npar parameters 38002 1.48e+03 38.0 1.52e+03 8 [ 0.357 0.202 21.810 5.117 0.798 0.454 4.600 0.010] Engines success reject failed best calls GalileanEngine 265627 81206 91904 39 38051 ChordEngine 266230 446883 0 53 38051 Calls to LogL 1151850 to dLogL 81206 Samples 38502 Evidence 640.648 +- 0.120
In[ ]:
Print parameters and standard deviations, first as they were derived and
then in an alternative form with angles in ``degrees'' and the
periastron in years.
In[8]:
sl = ns.samples
par = sl.parameters
std = sl.stdevs
pard = par.copy()
pard[3:] *= 180 / math.pi
pard[3] *= pard[2] / 360
pard[3] += 1900
stda = std.copy()
stda[3:] *= 180 / math.pi
stda[3] *= pard[2] / 360
names = mdl.parNames
print( " ", end="" )
for nm in names :
print( " %8.8s"% nm, end="" )
print()
print( "Pars ", fmt( par, max=None ) )
print( "Stdev ", fmt( std, max=None ) )
print( "Par_alt", fmt( pard, max=None ) )
print( "Std_alt", fmt( stda, max=None ) )
print( "Scale ", fmt( sl.scale ), "+-", fmt( sl.stdevScale ) )
print( "Evidence ", fmt( evi ) )
print( "periastron times" )
for k in range( -3, 6 ) :
print( fmt( pard[3] + k * par[2] ), end='' )
print()
Out[8]:
eccentri semimajo period phase si inclinat north2no nodes2pe
Pars [ 0.357 0.202 21.811 5.115 0.799 0.452 4.600]
Stdev [ 0.012 0.001 0.030 0.035 0.011 0.027 0.016]
Par_alt [ 0.357 0.202 21.811 1917.757 45.769 25.909 263.585]
Std_alt [ 0.012 0.001 0.030 0.122 0.647 1.568 0.909]
Scale 0.010 +- 0.000
Evidence 640.648
periastron times
1852.325 1874.136 1895.946 1917.757 1939.567 1961.378 1983.189 2004.999 2026.810
In[9]:
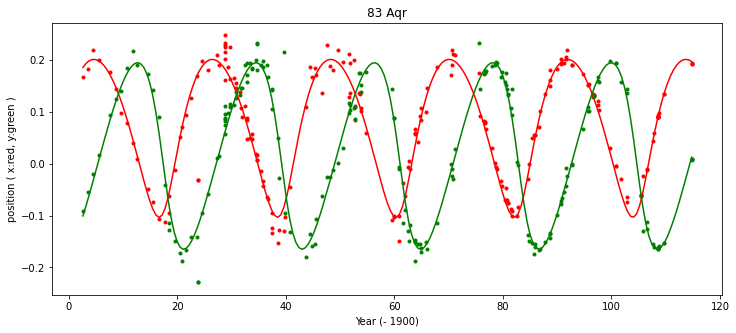
plt.figure( "results", figsize=(12,5) ) plt.plot( yr, xpos, 'r.' ) plt.plot( yr, ypos, 'g.' ) xx = numpy.linspace( yr[0], yr[-1], 201, dtype=float ) rp = mdl.result( xx, par ) xpf = rp[:,0] * numpy.sin( rp[:,1] ) ypf =-rp[:,0] * numpy.cos( rp[:,1] ) plt.plot( xx, xpf, 'r-' ) plt.plot( xx, ypf, 'g-' ) plt.xlabel( "Year (- 1900)") plt.ylabel( "position ( x:red, y:green )") plt.title( "83 Aqr" ) plt.show()
Out[9]:
In[10]:
plt.figure( "orbit", figsize=(6,6) )
mkrp = mdl.result( yr, par )
xmk = mkrp[:,0] * numpy.sin( mkrp[:,1] )
ymk =-mkrp[:,0] * numpy.cos( mkrp[:,1] )
q = numpy.where( yr0 <= 1900 )
plt.plot( xpos[q], ypos[q], 'k.' )
for k in q :
plt.plot( [xmk[k],xpos[k]], [ymk[k],ypos[k]], 'k-' )
q = numpy.where( numpy.logical_and( 1900 <= yr0, yr0 < 1950 ) )
plt.plot( xpos[q], ypos[q], 'b.' )
for k in q :
plt.plot( [xmk[k],xpos[k]], [ymk[k],ypos[k]], 'b-' )
q = numpy.where( numpy.logical_and( 1950 <= yr0, yr0 < 2000 ) )
#q = numpy.where( numpy.logical_and( 1990 <= yr0, yr0 < 2000 ) )
plt.plot( xpos[q], ypos[q], 'r.' )
for k in q :
plt.plot( [xmk[k],xpos[k]], [ymk[k],ypos[k]], 'r-' )
q = numpy.where( yr0 >= 2000 )
plt.plot( xpos[q], ypos[q], 'g.' )
for k in q :
plt.plot( [xmk[k],xpos[k]], [ymk[k],ypos[k]], 'g-' )
xx = numpy.linspace( yr[0], yr[-1], 201, dtype=float )
yy = mdl.result( xx, par )
xf = yy[:,0] * numpy.sin( yy[:,1] )
yf =-yy[:,0] * numpy.cos( yy[:,1] )
# plot the orbit
plt.plot( xf, yf, 'k-' )
#plot the center
plt.plot( [0.0], [0.0], 'k*' )
# plot line to periastron
yperi = mdl.result( [par[3] * par[2] / ( 2 * math.pi )], par )
xpr = yperi[0,0] * math.sin( yperi[0,1] )
ypr = -yperi[0,0] * math.cos( yperi[0,1] )
plt.plot( [0.0,xpr], [0.0,ypr], 'k-')
# plot line of nodes
xas = 0.3 * math.sin( par[5] )
yas =-0.3 * math.cos( par[5] )
plt.plot( [-xas,xas], [-yas,yas], 'm-')
plt.plot( [xas], [yas], 'ms' )
plt.axis('equal' )
plt.show()
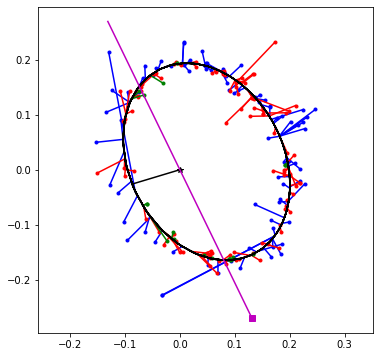
Out[10]:
In the picture above we see the orbit of 83 Aqr as it appears on the
sky. (North down, east left TBC). The black ellipse is the projected
orbit of the secundary star. It is moving anti-clockwise. The
observations at the colored points are connected to the orbit location
at the same time. The colors indicate when they are taken: blue < 1950;
1950 < red < 2000 and green > 2000.
The main star is located at (0,0) where the back * is plotted. Through
it in magenta is the line of nodes, i.e. where the sky through the main
star crosses the orbit. The magenta square indicates where the ascending
node is located, the place where the orbiting star crosses the sky plane
and is moving toward us. At the other side, at the descending node, the
orbiting star crosses the sky plane away from us. The black line from
the main star to the orbit indicate the lacotion of the periastron, the
place where the stars as closest together. The periastron lies behind
the sky plane.
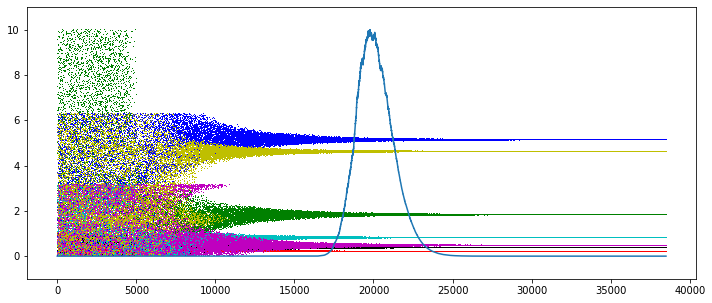
In[11]:
plt.figure( 2, figsize=[12,5] )
pev = sl.getParameterEvolution()
c = ['k,', 'r,', 'g,', 'b,', 'c,', 'm,', 'y,']
for k in range( mdl.npars ):
if k == 2 :
plt.plot( pev[:,k] - 20, c[k] )
else :
plt.plot( pev[:,k], c[k] )
wev = sl.getWeightEvolution()
wev /= numpy.max( wev )
plt.plot( wev * 10 )
plt.ylim( -1, 11 )
plt.show()