Radio Astronomy Spectrometer
Table 12.4 from Phil Gregory book is copied.NestedSampler is used to find the probability of a source present in the data.
Author: Do Kester
import stuff
In[1]:
import numpy as numpy import math from BayesicFitting import GaussModel from BayesicFitting import PolynomialModel from BayesicFitting import ConstantModel from BayesicFitting import NestedSampler from BayesicFitting import formatter as fmt from BayesicFitting import plotFit import matplotlib.pyplot as plt
In[2]:
x = [k for k in range(1,65)]
y = [0.82,-2.07,0.38,0.99,-0.12,-1.35,-0.20, 0.36,-.78,1.01,
0.44,0.34,1.58,0.08,0.38,-0.71,-0.90,0.33,0.80,-1.42,
0.28,-0.42,0.12,0.14,-0.63,-1.77,-0.67,0.55,1.98,-0.08,
1.16,0.48,-0.03,1.47,1.70,1.89,4.55,3.59,2.02,0.21,
0.05,0.54,-0.09,-0.61,2.49,0.07,-1.45,0.56,-0.72,0.38,
0.02,-1.26,1.35,-0.04,-1.45,1.48,-1.16,-0.40,0.01,0.29,
-1.35,-0.21,-1.67,0.70]
Define the model
In[3]:
mdl = GaussModel( ) print( mdl ) lo = [0,0,0] hi = [10,64,10] mdl.setLimits( lo, hi )
Out[3]:
Gauss: f( x:p ) = p_0 * exp( -0.5 * ( ( x - p_1 ) / p_2 )^2 )
define the fitter: Fitter
In[4]:
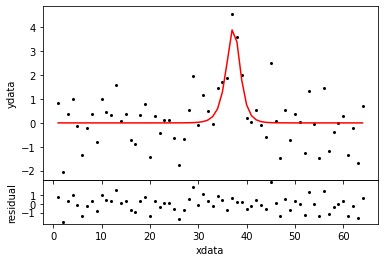
ns = NestedSampler( x, mdl, y ) ns.distribution.setLimits( [0.1, 10] ) evid = ns.sample( plot=True )
Out[4]:
Fit all parameters of
Gauss: f( x:p ) = p_0 * exp( -0.5 * ( ( x - p_1 ) / p_2 )^2 )
Using a Gauss error distribution with with unknown scale
Moving the walkers with GalileanEngine ChordEngine
>>>>>>>>>>>>>>>>>>>>
Iteration logZ H LowL npar parameters
1971 -98 9.9 -85.5 4 [ 3.922 37.210 1.590 0.900]
Engines success reject failed best calls
GalileanEngine 13833 4545 2861 12 1971
ChordEngine 13766 14430 0 5 1971
Calls to LogL 49435 to dLogL 4545
Samples 2071
Evidence -42.570 +- 0.136
In[5]:
sl = ns.samples par = sl.parameters
In[6]:
print( "Parameters :", fmt( ns.parameters ) ) print( "StDevs :", fmt( ns.stdevs ) ) print( "Scale :", fmt( ns.scale ) ) print( "Evidence :", fmt( evid ) )
Out[6]:
Parameters : [ 4.100 37.177 1.638] StDevs : [ 1.206 0.383 0.679] Scale : 0.963 Evidence : -42.570
How probable is the existence of a source with these parameters. Compare
it with a fit of a constant model, which is always 0.
In[7]:
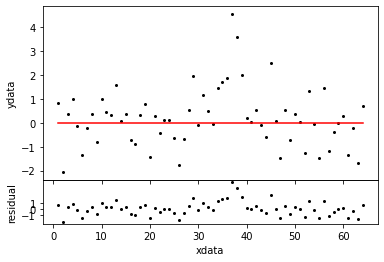
mdl0 = ConstantModel() ns0 = NestedSampler( x, mdl0, y ) ns0.distribution.setLimits( [0.1,10] ) evid0 = ns0.sample( plot=True ) sl0 = ns0.samples
Out[7]:
Fit all parameters of
ConstantModel: f( x ) = Polynomial: f( x:p ) = p_0
Using a Gauss error distribution with with unknown scale
Moving the walkers with GalileanEngine ChordEngine
>>>>>>
Iteration logZ H LowL npar parameters
553 -108 2.8 -104 1 1.236
Engines success reject failed best calls
GalileanEngine 3851 480 2 3 553
ChordEngine 3942 97 0 1 553
Calls to LogL 8372 to dLogL 480
Samples 653
Evidence -46.701 +- 0.072
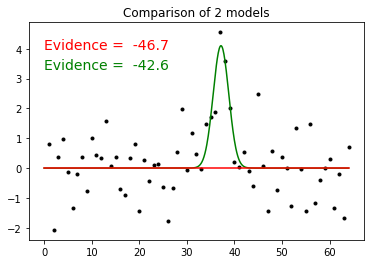
The log(evidence) decreased by 3.9, meaning that the GaussModel is
10^3.9 = 8000 times more probable than the constant model
In[9]:
plt.figure( 1 ) plt.plot( x, y, 'k.' ) xx = numpy.linspace( 0, 64, 641 ) plt.plot( xx, mdl.result( xx, par ), 'g-' ) plt.plot( xx, mdl0.result( xx, [] ), 'r-' ) txt1 = "Evidence = %6.1f" % evid txt0 = "Evidence = %6.1f" % evid0 plt.text( 0, 4, txt0, color='red', size=14 ) plt.text( 0, 3.3, txt1, color='green', size=14 ) plt.title( "Comparison of 2 models") plt.show() #plt.text( 13, 16.5, txt, size=14, # va="baseline", ha="left", multialignment="left", # bbox=dict(fc="none"))